Chemieklausuren, Arbeitsblätter und mehr: www.deinchemielehrer.de

Aufgabensammlung für das Fach Chemie in der Schule

Aufgaben mit Lösung: Elektrochemie

Alle Aufgaben mit LösungElektrochemie Organische Chemie

Übersicht - Elektrochemie Elektrolyse einer O,1mol/l Kupfersulfat-lösung an Kupfer- und an Platinelektroden Elektrochemische Bestimmung des Löslichkeitsproduktes von Silberchlorid AgClVergleich der Elektrolyse von 1 mol/l Salzsäure und von 0,001 mol/l Salzsäure an PlatinelektrodenPotentiometrische Titration einer Lösung mit versch. Halogenidionen mit 0,1 mol/l Silbernitratlösung. Elektrochemische Bestimmung des Löslichkeitsproduktes von Silberbromid AgBr Vergleich der Messung des Energieumsatzes der Reaktion von Ag+ - Ionen mit metallischem Eisenpulver in einem Kalorimeter und in einem galvanischen Element Reaktion von Silberionen mit metallischem Zink in wäßriger Lösung Elektrochemische Bestimmung des Löslichkeitsprodukts von Silberiodid Elektrolyse einer Kupferchloridlösung an Platin- und an Kupferelektroden Verhalten von Zink in der Lösung seines Salzes

Abstufung des Redoxpotentials der Halogene

Vergleich der Messung des Energieumsatzes der Reaktion von Ag⁺ - Ionen mit metallischem Eisenpulver in einem Kalorimeter und in einem galvanischen Element

In zwei Versuchen untersucht man den Energieumsatz von Ag⁺ - Ionen mit Fe.

Versuch 1

Im ersten Versuch setzt man 4 g Fe –Pulver mit 50 ml einer 0,5 mol/l AgNO₃ –Lösung in einem Becher aus Styropor um, der als Kalorimeter dient. Dabei bilden sich elementares Silber und Fe²⁺ - Ionen. Man misst folgende Temperaturen in Abhängigkeit von der Zeit:

Zeit (s)	0	15	30	60	75	90	105	120	135	150	165	180	195	210	225
T (°C)	20	20	20	20	28	37,5	47,5	53,5	53	52,5	51,3	50,5	49,5	49	48

Zeit (s)	240	255	270	285	300	330
T (°C)	47	46	55,5	44,5	43,5	42

Versuch 2

Im zweiten Versuch führt man die Reaktion von Versuch 1 in einem galvanischen Element durch. Man misst eine Spannung zwischen der Ag/ Ag⁺ - Halbzelle und der Fe/ Fe²⁺ Halbzelle von 1,24 V. Die Silberelektrode bildet dabei den + Pol.

Aufgaben

a) Stellen Sie das Versuchsergebnis von Versuch 1 graphisch dar und werten Sie die Graphik aus, indem Sie die Reaktionsenthalpie der Reaktion für Standardbedingungen bestimmen. Erläutern Sie Ihr Vorgehen und das hier angewandte Verfahren.

b) Zeichnen Sie das galvanisches Element, in dem die Messung von Versuch 2 durchgeführt werden kann. Beschriften Sie die Zeichnung.

c) Erläutern Sie die Vorgänge, die zur Ausbildung des elektrochemischen Potentials führen.

d) Berechnen Sie die freie Reaktionsenthalpie dieser Reaktion für Standardbedingungen. Erläutern Sie die Berechnung.

e) Berechnen Sie die Reaktionsentropie dieser Reaktion für Standardbedingungen.

f) Erläutern Sie die Aussagebedeutung der Reaktionsenthalpie, der freien Reaktionsenthalpie, der Reaktionsentropie sowie der Gleichgewichtskonstanten und interpretieren Sie die für diese Reaktion bestimmten thermodynamischen Daten insbesondere in Hinblick auf die Differenzen zwischen der Reaktionsenthalpie und der freien Reaktionsenthalpie.

Lösung

a) Zeichnung des Graphen

Bestimmung der Temperaturerhöhung nach dem dargestellten Verfahren, Berechnung der eingesetzten Stoffmengen und daraus Bestimmung der Reaktionsenthalpie:

Reaktionsschema:

eingesetzte Stoffmenge:

4 g Fe – Pulver entspricht 0,07 mol Fe

50 ml 0,5 mol/l AgNO₃ entspricht 0,025 mol Ag ⁺

Fe liegt damit im Überschuß vor, sodass ein vollständiger Umsatz gewährleistet ist

Aus den Messwerten ergibt sich folgende Graphik: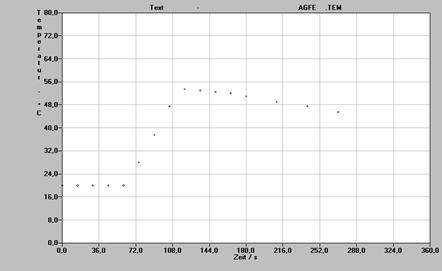

Somit hat man eine Temperaturerhöhung von 36 K.

Das ergibt einen Energieumsatz von

DH° =- 36^{-4,184 50}= 7531,2 J

eingesetzt wurden 0,025 mol Ag⁺ , damit ergibt sich der folgende Formelumsatz

DH°= - 7531,2 * 40 = - 301248 J

Die Standardreaktionsenthalpie beträgt also nach dieser Bestimmung DH° = - 301,2 kJ.

b) Skizzierung des Aufbaus des galvanischen Elementes, Beschriftung der Skizze

c) Erläuterung und Beschreibung der Vorgänge, die zur Ausbildung der Potential in einem galvanischen Element führen und daraus resultierend zu Ausbildung der gemessenen Spannung: unterschiedliche Lösungstension und Abscheidungstension der verschiedenen Metalle, Ursachen dieser Vorgänge, Bildung einer elektrischen Doppelschicht als Konsequenz daraus, Entstehung der gemessenen Spannung, Vorgänge am + Pol: Reduktion von Ag⁺ - Ionen zu Silber, am – Pol: Oxidation von Eisen zu Fe²⁺ Ionen.

d) Berechnung der freien Reaktionsenthalpie aus den Gesetzmäßigkeiten der Elektrochemie:

DG = - 2 * 96487 * 1,24

DG = - 239287 J/Formelumsatz

DG° = -239 kJ / Formelumsatz

Erläuterung der eingesetzten Werte,

e) Die Reaktionsentropie ergibt sich aus der Gibbs-Helmholtz-Gleichung:

DG = DH - T * DS

also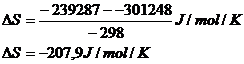

f) Erläuterung der Reaktionsenthalpie als der bei der Reaktion frei werdenden Wärme, die nicht vollständig in mechanische Energie umgewandelt werden kann, der freien Reaktionsenthalpie als der tatsächlich nutzbaren Energie und der Reaktionsentropie (bzw. Entropie) als das Maß für die Änderung der Unordnung. In diesem Fall ist die Reaktionsentropie negativ, daher wird die Ordnung bei der Reaktion größer. Dieses ist dadurch zu erklären dass aus zwei mol Ag⁺ - Ionen in hydratisierter Form 2 mol Silbermetall werden, aus einem gelösten Stoff wird hier also ein fester Stoff. Umgekehrt geht nur 1 mol Fe²⁺ in Lösung.